图小波神经网络

论文信息

• Paper: [ICLR 2019] Graph wavelet neural network[1]
• Link: https://arxiv.org/pdf/1904.07785.pdf

背景梳理

作者认为，对于已经在方方面大获成功的卷积神经网络CNNs而言，其包含一个潜在的先觉条件，即数据应是满足欧几里得结构的。对于大量的非欧数据而言，现阶段人们尝试将CNN推广至图数据科学，也即GCN。现阶段有两种主要方法来处理：一是遵循传统CNN做法的空间方法，直接在顶点域上定义卷积操作。对于每个顶点，卷积被定义为位于其邻域内所有顶点的加权平均函数，加权函数表征其邻居对目标顶点施加的影响。二是谱方法通过，图傅立叶变换和卷积定理定义卷积。谱方法利用图傅里叶变换将顶点域中定义的信号转换为谱域，例如图拉普拉斯矩阵的特征向量所跨越的空间，然后在谱域中定义滤波器，保持CNNs的权重共享特性。

对于谱方法(Spectral GNN)来说，其实际应用当中存在若干问题，可简单概括为以下几点：

• 谱方法的建模依赖于图拉普拉斯矩阵的特征值分解，具有很高的计算复杂度
• 谱方法中傅立叶基向量没有稀疏性，也导致了无法加速，计算效率低
• 谱方法中的傅立叶基向量是表示全局性的信号，不够突出其局部化的特征

为解决这些问题，本文提出图小波神经网络(GWNN)，即将谱方法图神经网络中的傅立叶基替换为小波基，作者认为其具有以下好处：

• GWNN和谱方法相比，不需要对拉普拉斯矩阵进行分解，有效降低了计算复杂度
• 图小波基稀疏的
• 图小波反映了以每个节点为中心的信息扩散。

信号处理中的傅立叶与小波

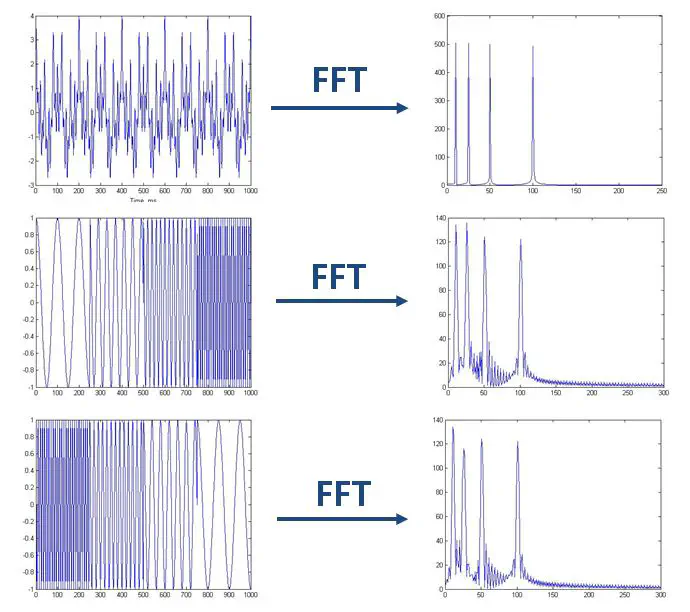
这里我们简单介绍一下在信号处理当中，小波基与傅立叶基的一些恩怨情仇。 为什么在傅立叶变换如此优美、且具有清晰物理含义的频谱分析方法提出后，我们还要发展相对而言更“黑盒”的小波呢？原因可以简单概括为，对于非平稳过程，傅立叶变换具有较大的局限性。 例如下图[2],左侧时域图表示了三个有较大差距的时域信号。对于第一个信号而言，其在整个时域中都具有相同的频谱分量，我们称之为“平稳的”。而后两个信号的频率则会随着时间的变换而发生改变。对三个差距巨大的信号进行快速傅立叶变换后我们发现，其频谱图却非常相似。 这说明傅立叶变换缺乏区分信号平稳性的能力，而现实世界中大量存在的正是非平稳信号，真正的平稳信号通常来自于人类刻意制造的信号发生器。为了解决这个问题，信号处理学家们提出了短时傅立叶变换(STFT，short-time Fourier transform)的概念：即对信号加窗，认为信号在一个很小的窗口内是平稳的，再对其进行傅立叶分析。但这也不是一个完美的解决方案，因为在窗长的选择上存在一个非常艰难的trade-off：如果窗长太长则导致其时间分辨率差，窗长太短则导致其频谱分辨率差。“我们无法同时获取一个信号（粒子）的频率（动量）时刻（位置）”堪称信号处理中的不确定性原理。这其中的巧妙联系也许正暗示了波粒二象性。(德布罗意波、物质波)

于是，聪明的信号科学家们又想出了新的办法。既然对于在整个时域都存在的傅立叶基来说，需要通过STFT这种操作来使其具有对非平稳信号的区分能力，我们为何不直接设计本身就是有限长的基呢？小波变化的基本思路便是“将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率信息，也可以知道频域所处的时间。

好了，这部分就介绍到这里，下面我们继续看GWNN的内容。

图小波变换

与图傅立叶变换类似，图小波变换将图信号从vertex域映射到spectral域。图小波变换将一组小波设为基：

其中表示图信号中由节点扩散出的部分，则是一个缩放因子。

其中是拉普拉斯特征向量组成的矩阵，则是一个缩放矩阵，其中。 图信号的小波变换可写作

逆变换可写作：

其中 可以简单地将中的换成来得到。与图傅立叶变换类似，我们可将卷积操作定义为：

与图傅立叶变换相比，这样定义的图小波变化有什么好处呢？

• 1、可以通过快速算法来获得图小波而不需要拉普拉斯矩阵的特征分解，其具体方法请参考[3]
• 2、对于现实世界中的图信号，矩阵和均具有高度的稀疏性：例如在Cora数据集中，中97%的元素均为0。
• 3、每个小波对应于从中心节点扩散的图信号，在顶点域中具有高度的局部化特征。（详见文章附录A）
• 4、图小波变换可以更灵活地调整节点的邻居。可以利用连续的方式，即改变缩放参数s来改变邻域的范围。

图小波神经网络

将傅立叶变换替换为小波变换，GWNN可以视作一个多层的卷积神经网络。其第层的结构为：

根据该式，每层GWNN的参数复杂度为。其中n是图节点的数量，p是本层的特征通道数，q是下一层的特征通道数。传统的 CNN 方法为每对输入特征和输出特征学习卷积核。 这导致了大量的参数，并且通常需要大量的训练数据来进行参数学习。 这对于基于图的半监督学习是不可接受的。 为了解决这个问题，本文将特征转换与图卷积分离。 GWNN 中的每一层都分为两个组件：特征变换和图卷积。

实验

作者在半监督节点分类任务上验证了模型的性能，其中包括三个数据集：Cora，Citeseer，Pubmed。与其与方法的比较可由下图所示： 作者也对傅立叶和小波的稀疏性进行了比较，结果如下所示： 可见小波基在稀疏性上具有压倒性的优势。

参考文献

[1]: Xu, Bingbing, et al. "Graph wavelet neural network." arXiv preprint arXiv:1904.07785 (2019).

[2]: 形象易懂讲解算法I——小波变换 https://zhuanlan.zhihu.com/p/22450818

[3]: David K Hammond, Pierre Vandergheynst, and Re ́mi Gribonval. Wavelets on graphs via spectral graph theory. Applied and Computational Harmonic Analysis, 30(2):129–150, 2011.